nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度。 将Momentum 中的公式展开可得：

$$\Delta{\thetat}=-\eta\mum{t-1}-\eta*gt$$ 可以看出，$$m{t-1}$$ 并没有直接改变当前梯度$$g_t$$。

Nesterov的改进就是让之前的动量直接影响当前的动量。即：

$$gt=\nabla{\theta{t-1}}{f(\theta{t-1}-\eta\mum_{t-1})}$$

$$mt=\mu*m{t-1}+g_t$$

$$\Delta{\theta_t}=-\eta*m_t$$

所以，加上nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。如下图：

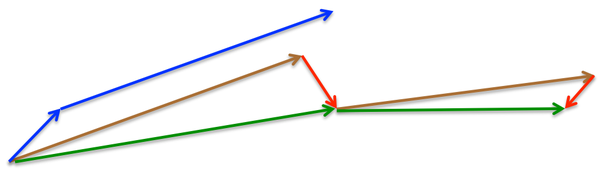
momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

其实，momentum项和nesterov项都是为了使梯度更新更加灵活，对不同情况有针对性。但是，人工设置一些学习率总还是有些生硬，接下来介绍几种自适应学习率的方法